Meet the family
Our range of plug’n’play products
for watching live and recorded TV
around your home.
WHAT Can I Watch?
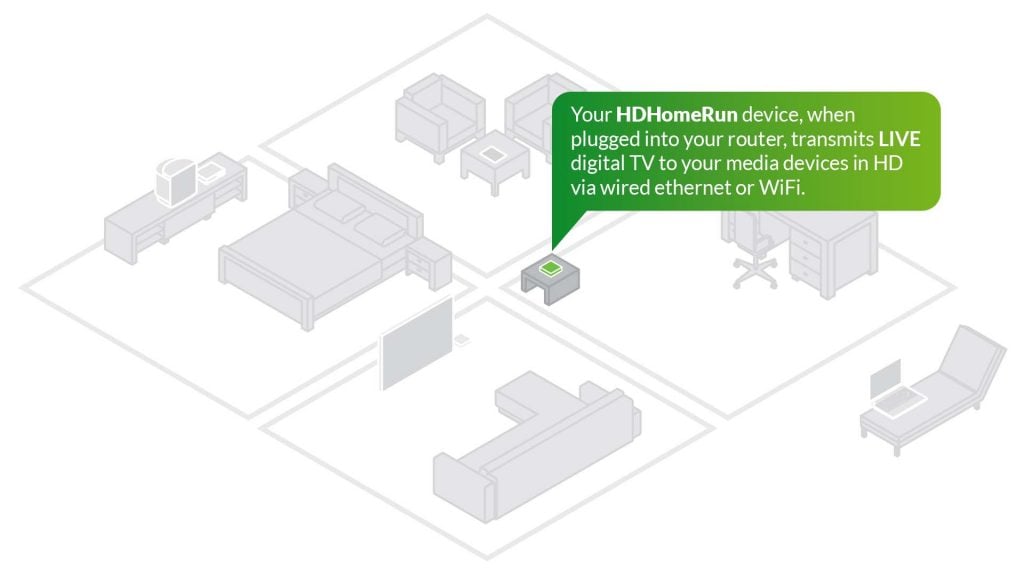
Watch Live HDTV on your computers, portable media devices and smart TV media boxes.
IT’S FOR EVERYONE.
Compatible with all your favorite smart devices – it’s HDTV that the whole family can enjoy.
Cut that cord.
Cut the cable expenses with an antenna and FREE local TV! Over a year, that really makes a HUGE saving!
* Sample channels shown. Check availability in your area.
Catchup with your favorite team.
With our subscription DVR solution you can set it to record all the games that only your team play, so you never miss a match again.
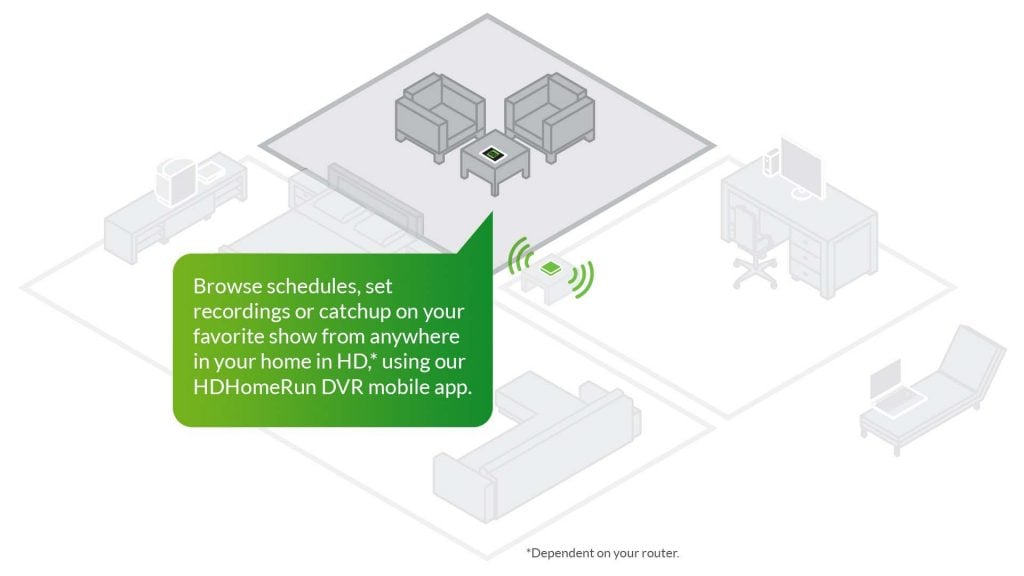
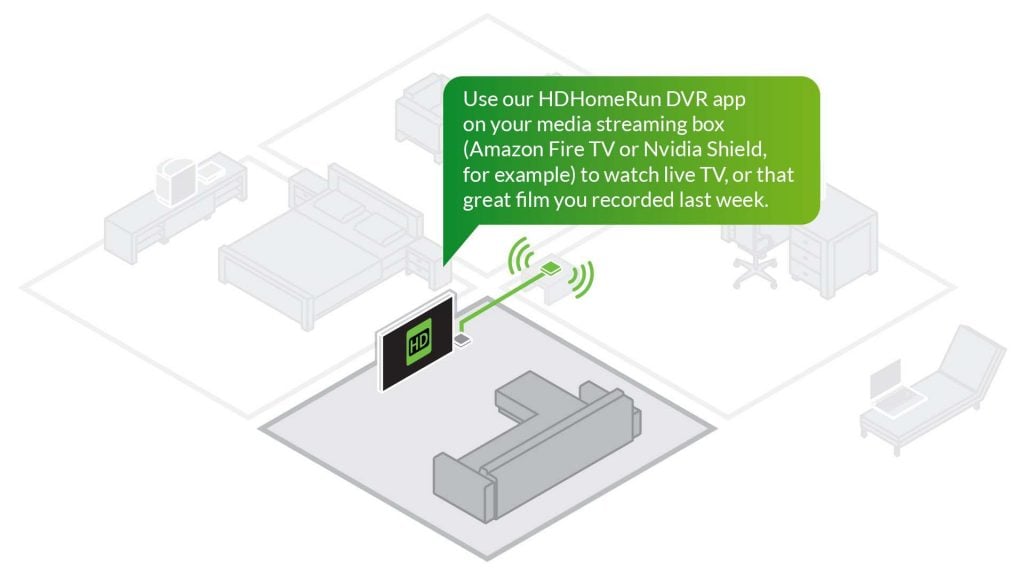
Once you’ve scheduled it to record, you can watch wherever you want in your home. To watch in the lounge, simply use a media streaming box or compatible smart TV to watch on the big screen.
The choice is all yours.
How does it work?
ATSC 3.0 TV
Compatible with all your favorite smart devices – it’s HDTV that the whole family can enjoy.
Consoles. Not just for games.
With our HDHomeRun app you can watch live HDTV on your games console or smart media box. Simply load up our app from the appropriate store, and your box becomes your one device for games, entertainment and, most importantly, live HDTV.
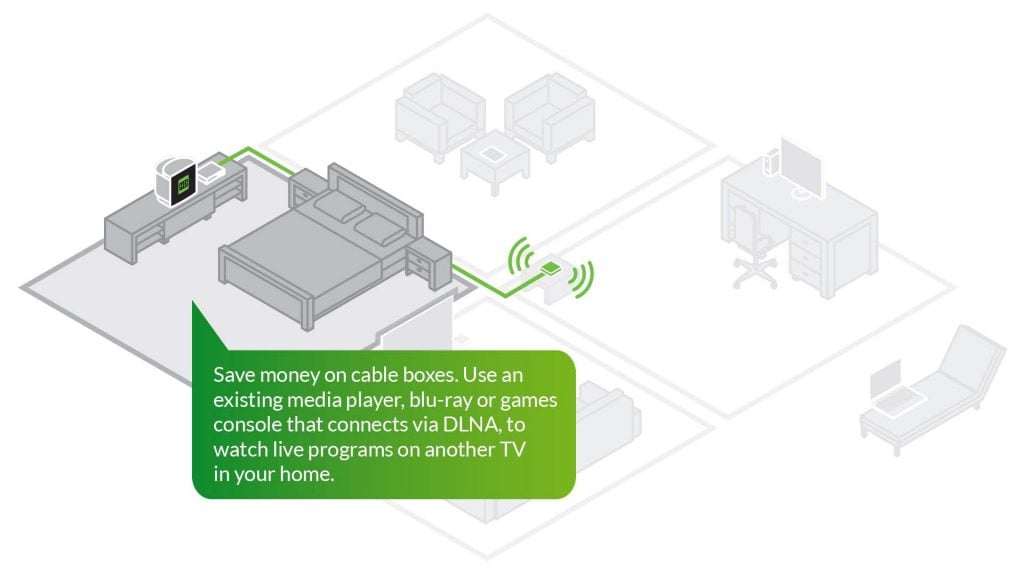
And if you have subscription cable (US only), you can watch protected content too. So you can cut down on cable boxes that you need to rent.
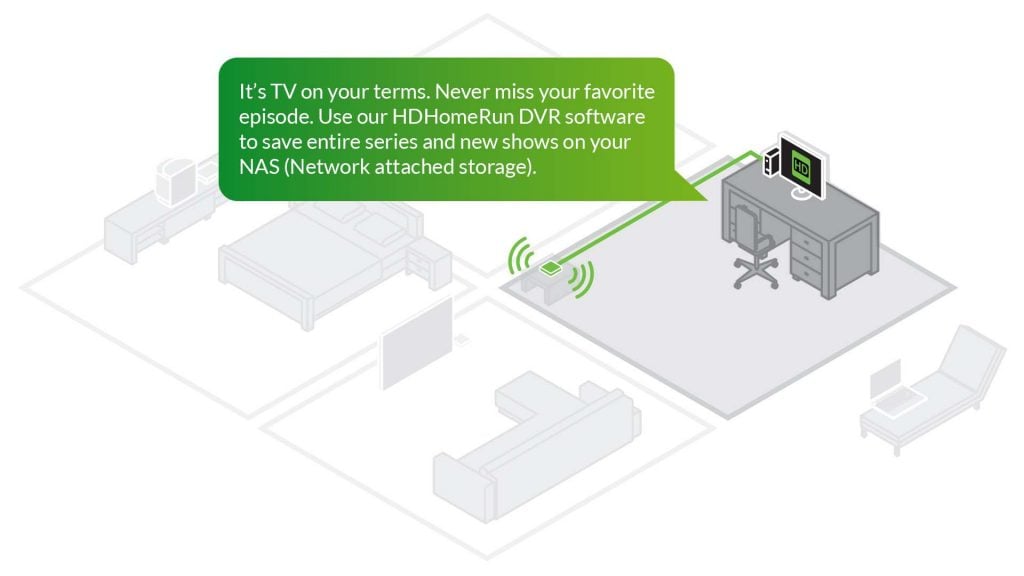
So, what is the HDHomeRun DVR solution?
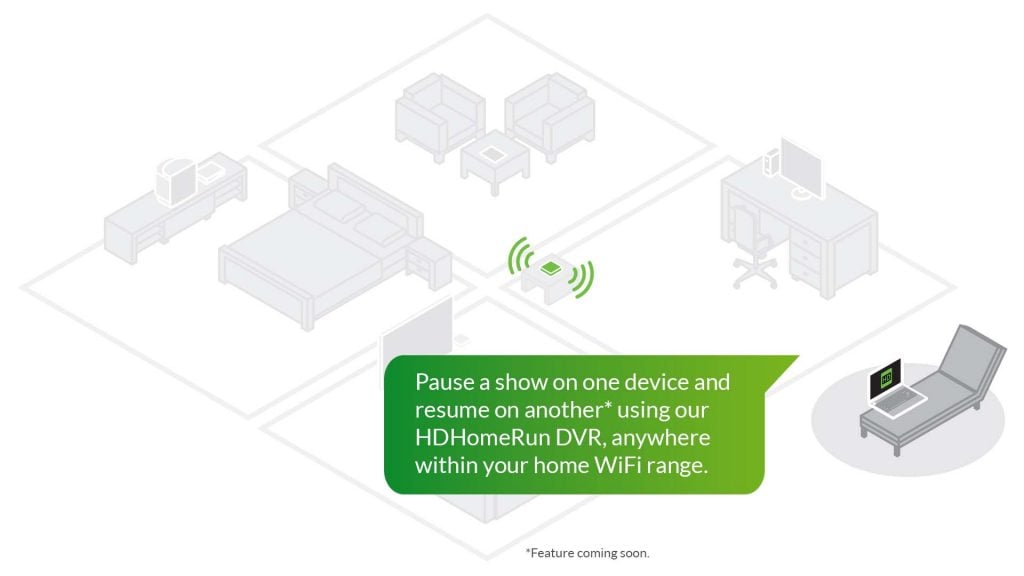
Not just one TV – now you can watch TV on all the smart screens in your home.
Zero configuration! From a single smart TV to as many devices as you want – everything is auto-detected and works together as one DVR. Your home network becomes your DVR.
No more recordings stuck inside one box. No more being forced to watch on the one TV that does DVR. This is TV the way you want. On your terms.
Don’t buy another HDMI box. You already have it – use your favorite Android TV, Fire TV, Apple TV, Roku, XBox, iOS, LG, Windows, Mac devices you already own and enjoy.
Never run out of tuners to record shows – you can add any number of HDHomeRun tuners on your network and they all work together as one DVR.
Never run out of recording space – you can add any number of HDHomeRun FLEX tuners with USB attached hard drives, any number of network attached storage (NAS) devices, and any number of Windows/Mac/Linux PCs acting as storage – the combined storage works as one big storage pool for DVR recording.
It’s a re-imagined DVR solution. It can be as simple as a laptop or as expansive as a multi-client, multi-NAS, multi-tuner masterpiece.
Install the app and you are running. Give it a few recording tasks and it goes to work.
So, how does the DVR service work?
DECIDE ON YOUR SOURCE
For Cord Cutters – FREE Over the air TV is received via antenna. For Cord Shavers – Cable TV is received via digital cable subscription.
CHOOSE YOUR HDHOMERUN PRODUCT
Use HDHomeRun FLEX for FREE over the air TV. Use the HDHomeRun FLEX 4K for the ATSC 3.0 future. Use HDHomeRun PRIME for digital cable TV and save on multiple box rental fees
SETUP RECORDED STORAGE
Connect a USB hard drive to your HDHomeRun FLEX or use existing network storage for recorded content like your PC , Mac, or NAS.
DOWNLOAD THE HDHOMERUN DVR APP
Download our free app, available from our download page for desktop, or from all the popular app stores for smart devices.
HDHomeRun products available in your region
Features at a glance
It’s available for all your favorite devices & platforms
WINDOWS UNIVERSAL
Our Universal App is available for all WINDOWS Devices. Minimum specification: 2Gb RAM, Dual Core x86.
Can play Live DRM protected content from your cable provider included in your cable subscription.
WINDOWS 10/11
XBOX ONE and above
SURFACE TABLET
ANDROID
Can play Live DRM protected content from your cable provider included in your cable subscription.
NVIDIA SHIELD TV
ANDROID PHONE
ANDROID TABLET
ANDROID TV
APPLE
Our App is available for Apple desktop, laptop devices, iPads and iPhones, with a minimum specification: OSX 10.11, 2Gb RAM, Dual Core x86, iOS version 11 minimum (works with all HDHomeRun products). Can play Live DRM protected content from your cable provider included in your cable subscription on iOS only. DRM content viewing for MacOS and TVOS coming soon.
Mac Computers
Macbooks
iPhones / iPads
Apple TV
AMAZON FIRE TV
Our App is available for compatible Amazon Fire devices, Fire TV OS television and Fire TV Stick (Gen 2).
AMAZON FIRE TV BOX
AMAZON FIRE TV STICK (GEN 2)
AMAZON FIRE TV EDITION
ROKU
Our App is available for compatible ROKU devices – ROKU Ultra and ROKU TVs.
ROKU Ultra
ROKU TV
3RD PARTY MEDIA CENTER APPLICATIONS
These 3rd party software solutions run on many different platforms, and support live TV from our hardware.
PLEX
EMBY
CHANNELS
ATSC 3.0 DRM: Some ATSC 3.0 channels may be DRM encrypted and will not work. If an ATSC 3.0 channel is DRM encrypted the HDHomeRun FLEX 4K will use the ATSC 1.0 version of the channel. DRM encryption is used by select broadcasters to block out-of-home viewing, limit what player devices can be used to watch TV, enforce that the original tuner hardware is always present to view recordings, and to block third party apps. Optionally a broadcaster can force recordings to expire after a period of time and/or block recording completely.
Compare all our products on one, easy to use comparison chart.
Sports bar, hotel or restaurant? We’ve got a business solutions to suit your needs.